Variational Autoencoder
Table of Contents
With autoencoder, the same latent variable \(z\) gives the same output \(\hat{x}\) because the decoding is deterministic. VAEs introduce stochasticity so that new samples can be generated.
This is done by breaking down the latent space \(z\) to a mean vector (\(\mu\)) and standard deviation vector (\(\sigma\)). The encoder outputs \(\mu\) and \(\sigma\) from which \(z\) can be sampled.
1. VAE Loss
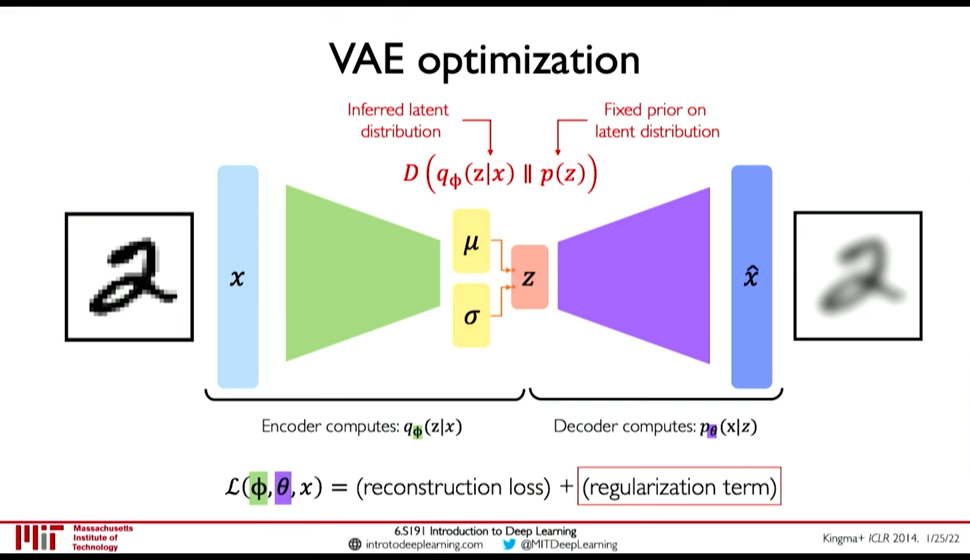
Figure 1: VAE optimization
Loss function \(L(\phi, \theta, x)\) is reconstruction loss + regularization term.
- Encoder computes: \(q_{\phi}(z|x)\) i.e. the distribution of latent representation given the input image
- Decoder computes: \(p_{\theta}(x|z)\) i.e. the distribution of images given the latent representation
- Reconstruction loss: log-likelihood (?), \(||x-\hat{x}||^2\)
Regularization Loss:
Regularization loss: \(D(q_{\phi}(z|x)\ ||\ p(z))\) is divergence in the two probability distribution.
- \(q_{\phi}(z|x)\) is inferred latent distribution
- \(p(z)\) is a prior distribution on the latent space
- A common choice for the prior is a Normal Gaussain distribution
- Encourages encodings to distribute evenly around the center of the latent space
- Penalize the network when it tries to "cheat" by clustering points in specific regions (i.e. by memorizing the data)
We use Regularization function so that:
- Latent space is continuous
- Latent space is Completeness: Sampling from latent space must give meaningful content
If regularization is not enforced:
- variance can be small and
- means may be distributed far apart so that there is no meaningful content in between
However, greater Regularization can adversely effect the reconstruction. So, a balance is needed.
2. Optimization
Backpropagation cannot be done through Sampling operation. So, we have to use a clever idea: Reparametrize the sampling layer \(z \sim N(\mu, \sigma^2)\) as \(z = \mu + \sigma \times \epsilon\) where \(\epsilon\) is sampled stochastically.
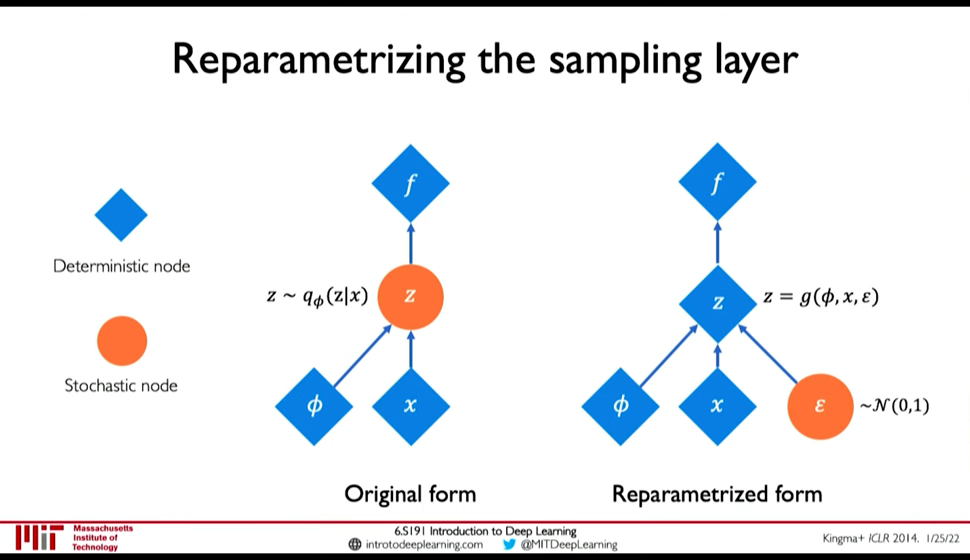
Figure 2: Reparametization of Sampling Layer
3. Disentanglement \(\beta\) -VAEs
We want latent variables that are uncorrelated with each other. \(\beta\) -VAEs achieve this by enforcing diagonal prior on the latent variables to encourage independence.

Figure 3: \(\beta\) -VAEs
4. Resources
- https://mbernste.github.io/posts/vae/
- MIT 6.S191: Introduction to Deep Learning
- A Recipe for Training Neural Networks: https://karpathy.github.io/2019/04/25/recipe/